Convolution Layer with Numpy
Basic Forward and Backward Propagation of Convolution Layer in Python
Convolution layer
In the field of image processing, the Convolution layer is the core building block of a Convolutional Neural Network. The primary purpose of Convolution layer is to extract features from the input image. The Convolution layer parameters consist of a set of learnable filters (kernels or feature detectors).
Filters are used for recognizing patterns throughout the entire input image. Convolution works by sliding the filter over the input image and along the way we take the dot product between the filter and chunks of the input image.
Matrix and Tensor
Matrix is a tabular format in which numbers can be represented. Tensor is like a function, i.e. is linear in nature. It describes an object that is in space. Tensors are of different types. 0 Rank tensors is scalars. 2nd Rank tensors is 2-D arrays which is a matrix.
im2col and col2im
im2col
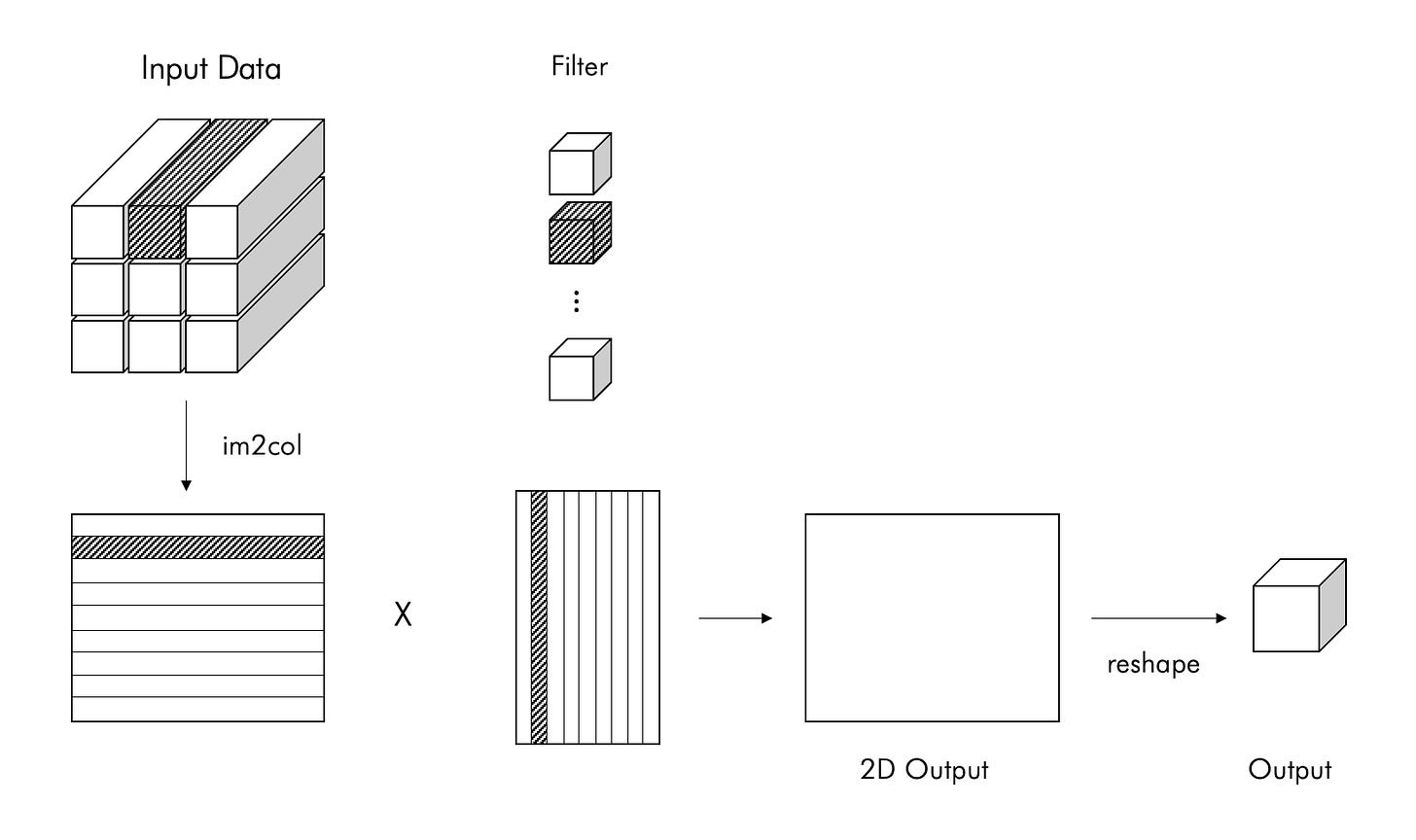
im2col is a technique where we take each window, flatten it out and stack them as columns in a matrix. The current general convolutional layer acceleration method is to use the image to column (im2col) algorithm to split the input image into a column matrix, then use the general matrix multiplication (GEMM) to perform matrix multiplication on the column vector and the convolution kernel.
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_ Data: input data composed of 4-dimensional arrays (data volume, channel, height and length)
filter_ H: filter high
filter_ W: length of filter
Stripe: stride
Pad: fill
Returns
-------
Col: 2-dimensional array
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
After expanding the input data with im2col, you only need to expand the filter (weight) of the convolution layer vertically into one column and calculate the product of the two matrices.
The weights of the convolution layer are similarly stretched out into rows. After the image and the kernel are converted, the convolution can be implemented as a simple matrix multiplication.
col2im
col2im operation is needed during back propagation. This is for reshaping this multiplied matrix back to an image at the end.
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
col :
input_ Shape: the shape of the input data (for example: (10, 1, 28, 28))
filter_h :
filter_w
stride
pad
Returns
-------
"""
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
Convolution Layer
Convolution Layer is consist of forward and backward propagation.
def __init__(self, W, b, stride=1, pad=0):
"""
Parameters
----------
w : filter
b : bias (vector)
"""
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# temporary variables in backward()
self.x = None
self.col = None
self.col_W = None
# gradient of weight and bias
self.dW = None
self.db = None
Forward Propagation
After expanding the input data with im2col, you need to expand the filter (weight) of the convolution layer vertically into one column and calculate the product of the two matrices.
def forward(self, x):
"""
Parameters
----------
x : input data (4D tensor)
FN : filter no.
C : channel
FH : filter height
FW : filter width
self.W : filter (4D tensor)
N : the number of input data in a batch (Batch size)
H, W : height and width of input data
out_h, out_w : height and width of ouput data (after convolution)
-------
out : output images
"""
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
Backward Propagation
As for the code of back propagation of convolution layer, col2im is used, which is the inverse process of im2col.
The transpose operation will change the order of the axes of the multidimensional array. For example, transpose (0, 3, 1, 2) is to change the axes of the original 0, 1, 2, 3 positions to the positions of the input parameters.
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
Convolution is a simple mathematical operation that is fundamental to many common image processing operators. I hope this post help you do a great exercise using the convolution layer from scratch.